Le rachat permet au souscripteur de disposer d’une partie ou de la totalité de son épargne avant l’échéance de son contrat. Pour un assureur, une mauvaise estimation de ces rachats peut accroître le risque de liquidité et engendrer des difficultés en termes de gestion actif-passif. Le rachat total met en outre fin aux contrats : les frais de gestion ne sont alors plus prélevés. Tous ces coûts expliquent l’intérêt porté par les actuaires aux méthodes de prédiction des rachats. Plusieurs de ces méthodes s’appuient sur des modèles statistiques de classification binaire (0 : le souscripteur ne rachète pas son contrat, 1 : le souscripteur rachète son contrat). L’évaluation de ces modèles se fait en général par le biais d’approches statistiques comme la précision, le F-score ou l’AUC.

L’apport du travail de Pierrick Piette et Stéphane Loisel est d’abord d’utiliser de nouveaux algorithmes tels que le XGB et les SVM pour la prédiction. Cependant, l’élément principalement mis en avant au cours de leur présentation est la possibilité d’évaluer le gain financier impliqué par chaque modèle et donc de replacer la dimension économique du problème des rachats au centre du processus de prédiction. Pour cela, ils apprécient la pertinence des algorithmes en termes d’efficacité économique, dans le cadre d’un système d’incitation des assurés à rester en portefeuille, plutôt qu’en termes de qualité de la prédiction binaire du rachat total.

Pierrick Piette expose les principaux apports de ce travail de recherche, notamment en matière de gestion des risques, ses avantages par rapport aux méthodes usuelles mais aussi ses difficultés de mise en œuvre.

L’approche statistique classique

Modéliser le comportement d’un client pour savoir si oui ou non il va réaliser une action est un problème bien connu des actuaires. Il peut être abordé par bon nombre de modèles dont les arbres de décisions ou la régression logistique.

D’autres, moins connus, ont été également choisis par les auteurs pour leur performances avérées sur ces problématiques et leur approche différente.

Le SVM, Support Vector Machine, est un algorithme de classification qui cherche à créer deux catégories en les séparant par un hyper plan. La problématique principale est donc de déterminer quelle est la frontière optimale parmi tous les hyperplans candidats. L’algorithme recherche celui qui maximise la distance entre les individus et cette frontière, c’est un problème d’optimisation.

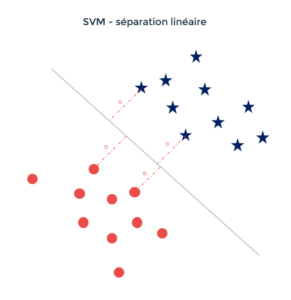
Cependant, il est très fréquent que les données ne soient pas linéairement séparables. Il existe une astuce dite « du noyaux » (Kernel Trick) qui permet d’appliquer une transformation aux données pour revenir à une situation favorable au SVM. Tout l’enjeu repose sur la détermination de cette transformation sur les données testées.

Autre modèle utilisé, le XGBoost (eXtreme Gradient Boosting) repose quant à lui sur une combinaison de plusieurs méthodes.

  • Le gradient tree boosting, apprentissage itératif sur les erreurs de catégorisation faites par des arbres de décisions « faibles » (peu de profondeur et peu de feuilles). L’idée étant d’attribuer des poids importants aux individus mal catégorisés et d’optimiser ces poids via la méthode de descente du gradient pour minimiser une fonction de perte (fonction de perte logistique dans ce cas).
  • Introduction d’aléatoire dans chaque nouvel arbre que ce soit au niveau des observations sélectionnées (comme le bagging) ou des variables explicatives (comme les forêts aléatoires).

Comment mesurer la performance statistique de ces modèles ?

Le protocole suivi par les auteurs pour entraîner et tester les modèles est classique en Machine Learning.

La base de données initiale a tout d’abord été partitionnée aléatoirement en 10 sous échantillons de même taille. L’apprentissage est ensuite réalisé sur chacun d’eux avant d’appliquer le modèle à la table de test (créée en retirant les observations de la table d’apprentissage à la base de données globale).

La précision des modèles est testée à l’aide d’une matrice de confusion permettant de compter simplement le nombre de vrai positif (prédiction de rachat alors que le client a racheté), le nombre de vrai négatif (prédiction de non rachat alors que le client n’a pas racheté) et le nombre d’erreurs.

La somme des « vrai positif » et des « vrai négatif » ramené au nombre total d’individus de la base de données permet d’obtenir la précision du modèle testé (pourcentage de bonnes classifications). Les résultats sont affichés dans le tableau ci-dessous.

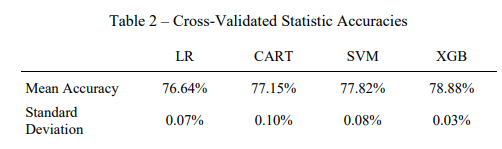
Comment mesurer l’impact financier des modèles de Machine Learning ?

Bien qu’évaluer les modèles grâce à des métriques statistiques permette d’avoir une idée de quels contrats risquent d’être rachetés, le risque de rachat reste avant tout un risque économique. Un des apports majeurs du travail de MM. Piette et Loisel est d’avoir pris en compte cette dimension économique lors de l’évaluation de leurs modèles.

En marketing quantitatif, la Customer Lifetime Value (CLV), aussi appelée Valeur Vie Client, est un indicateur qui correspond à la somme des profits générés par une entreprise tout au long de sa relation avec un client. Il est possible d’appliquer cela au secteur de l’assurance vie afin d’estimer la perte financière impliquée par le rachat d’un contrat par un client.

Cette notion permet également d’aller plus loin, c’est-à-dire de ne pas seulement constater le montant des pertes mais d’évaluer les gains éventuels d’une politique visant à retenir les clients susceptibles de racheter.

La mesure finale, qui intègre la politique de rétention, doit notamment tenir compte des éléments suivants :

  • Le ratio de profitabilité des contrats, ici supposé fixe d’un contrat à l’autre, ainsi que leur valeur nominale.
  • La récompense proposée aux clients considérés comme susceptibles de racheter leur contrat pour qu’ils ne le fassent pas. Cette récompense est ici également fixée à un même niveau pour tous les contrats et implique une diminution de la profitabilité du contrat si elle est acceptée.
  • La probabilité que les clients désireux de racheter leur contrat ne le rachètent pas et acceptent la récompense (gain de rétention). Si la récompense est proposée à un client qui ne souhaitait pas racheter son contrat, alors ce dernier accepte obligatoirement la récompense (perte liée à un mauvais ciblage des clients).
  • Le coût de contact des clients, également fixe. Ce coût incite à ne pas contacter trop de clients.

Pour que le modèle soit financièrement intéressant, il faut donc que les gains liés à la rétention de clients désireux de racheter soient supérieurs au coût de contact et à la perte liée au mauvais ciblage des clients.

L’utilisation de cette nouvelle mesure de performance accroît l’intérêt du XGB et des SVM par rapport aux modèles de régression logistique (LR) et CART. En effet, les gains de rétention permis par les deux algorithmes introduits par MM. Piette et Loisel sont bien supérieurs à ceux des deux autres modèles.

***

Retrouvez le document de recherche complet de Pierrick Piette, Stéphane Loisel et Jason Tsai :

« Applying economic measures to lapse risk management with machine Learning approaches »

 

NB. Pour entraîner les modèles, c’est une base de données sur des produits d’assurance vie taïwanaise qui a été utilisée. Elle regroupe 630 000 polices d’assurance entre 1998 et 2013 et contient le dernier statut connu de la police (normal, rachat, décès de l’assuré, …) ainsi que la date de changement de statut. Il est bon de noter qu’il n’y a pas de rachat partiel ces données.