Introduction
L’assurance automobile, qui a représenté 11,6% des cotisations d’assurance en France en 2020 d’après les chiffres de la Fédération Française de l’Assurance [1], est une assurance obligatoire. Ses enjeux stratégiques croissent à mesure que le parc automobile augmente en France (+ 5,2 millions de véhicules entre fin 2014 et fin 2020, toujours d’après la FFA). Dans ce contexte, un positionnement tarifaire adéquat offre un avantage concurrentiel réel pour les acteurs du marché.
Dans cette optique tarifaire, la notion de « zone » intervient régulièrement. La prime payée par l’assuré dépend, en partie, de sa localisation géographique. La constitution d’un « zonier » pertinent est donc souvent intéressante pour l’assureur, mais pas toujours efficace lorsqu’elle s’appuie sur des données statiques.
Dans cet article, nous proposons une méthode simple de partitionnement de séries temporelles qui permet, en partie, de répondre à cette problématique. Les données utilisées, en open source, concernent les accidents corporels de la circulation routière en France métropolitaine.
Données utilisées
Nos travaux s’appuient sur des jeux de données gouvernementales qui répertorient l’ensemble des accidents corporels de la sécurité routière en France pour les années 2005 à 2020. Ces données fournissent des informations relatives à la localisation des accidents, à leurs caractéristiques, aux types de véhicules impliqués (voitures, camions, vélos, etc) ainsi qu’aux victimes déclarées. Le Graphique 1 indique le nombre d’accidents répertoriés en France métropolitaine par année dans la base de données. Ces éléments sont identiques à ceux fournis par l’Observatoire national interministériel de la Sécurité routière.
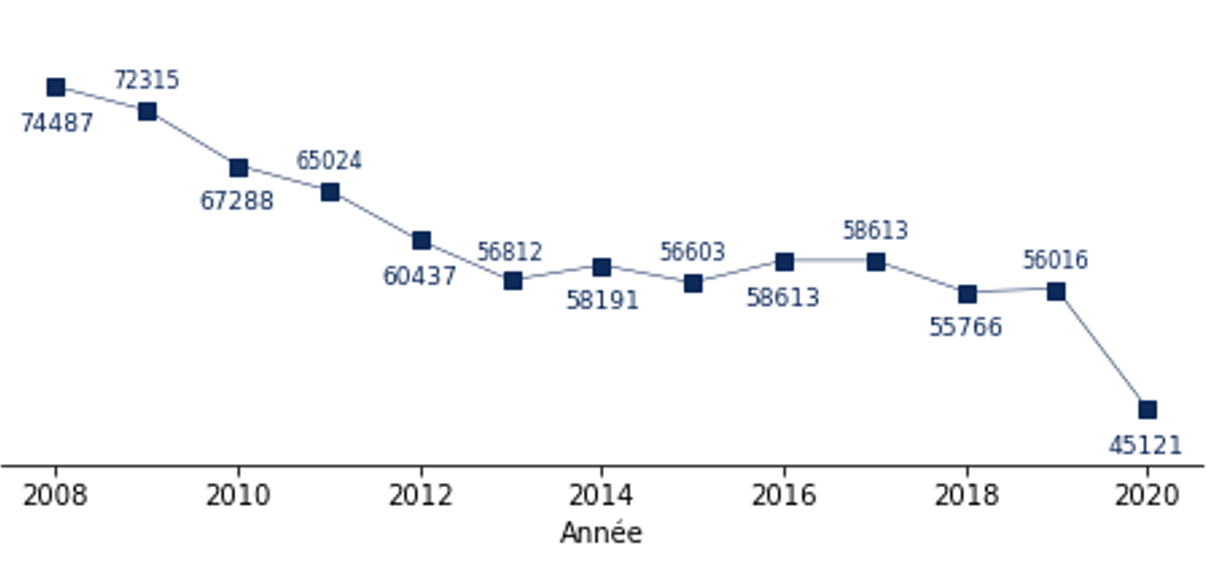
Graphique 1 : nombre d’accidents en France métropolitaine.
À partir des données récupérées, nous avons construit un ensemble de séries temporelles qui donnent, pour chaque département de France métropolitaine, le nombre mensuel d’accidents de la route de 2012 à 2020. La comparaison immédiate de ces séries n’est cependant pas pertinente. En effet, l’exposition au risque (temps total passé sur la route) diffère selon les départements.
En l’absence de cette exposition à la maille adéquate, nous nous sommes appuyés sur les données annuelles du parc automobile français pour homogénéiser les séries. Nous avons rapporté le nombre d’accidents observés au cours d’un mois pour un département donné au nombre de véhicules dans ce département pour ce mois. Les données sur le parc automobile étant annuelles, une linéarisation permet d’obtenir le nombre de véhicules mois par mois. Les données sur le parc automobile n’ayant pas la même profondeur d’historique que les données sur les accidents, nous avons limité notre période d’observation à 2012-2020.
Méthodologie adoptée
L’exploration préliminaire des données ainsi mises en forme a mis en exergue la disparité géographique des accidents corporels de la route en France métropolitaine. A titre illustratif, le Graphique 2 indique l’évolution observée pour les départements de l’Ain (courbe bleue), de l’Allier (courbe marron) et des Alpes-Maritimes (courbe rouge). Si l’on observe une certaine homogénéité entre l’Ain et l’Allier, le contraste avec les Alpes-Maritimes est très visible.
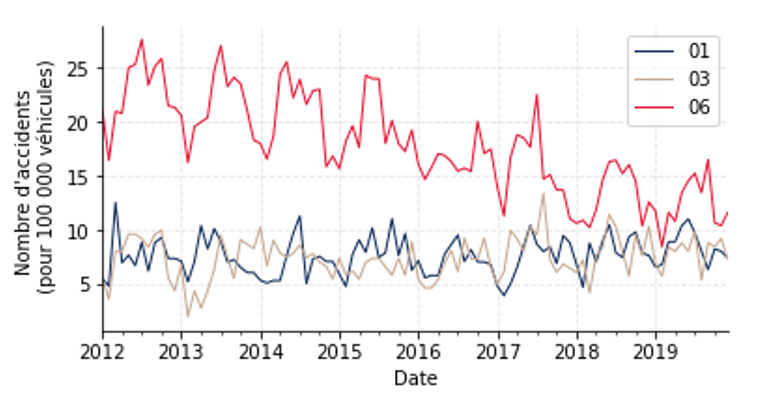
Graphique 2 : évolution temporelle du nombre d’accidents pour les départements de l’Ain, de l’Allier et des Alpes-Maritimes.
Regroupement des séries temporelles
Nous avons ensuite cherché à regrouper les différentes séries temporelles en plusieurs catégories. Il s’agit ici d’un problème de classification non supervisée. Il n’existe pas de variable à prédire, mais simplement un regroupement à effectuer de la manière la plus pertinente possible.
Dans cette optique, nous avons utilisé l’algorithme K-means, très classiquement utilisé dans ces problématiques de partitionnement. Le principe est de créer un nombre k (fixé) de partitions initialisées aléatoirement. Ces partitions représentent la position moyenne des observations du dataset. On associe ensuite chaque observation à la partition dont elle est la plus proche pour une distance donnée. Puis on recalcule la moyenne pour chaque partition. Cela est répété jusqu’à ce qu’il y ait convergence et que les moyennes n’évoluent plus.
La spécificité de notre cas d’usage réside dans le fait de travailler sur des séries temporelles et non sur des données ponctuelles. Cela permet de prendre en compte le niveau mais également la tendance dans le regroupement des séries temporelles.
Distance retenue et nombre de partitions
Deux éléments apparaissent donc déterminants pour la classification : la distance retenue et le nombre de partitions choisi. Dans certains cas d’usage, en particulier lorsque les séries temporelles ne sont pas comparables directement point par point (par exemple parce qu’il existe un décalage entre elles), il peut s’avérer utile d’utiliser le Dynamic Time Warping [2], qui cherche à aligner temporellement les séries pour minimiser la distance euclidienne entre elles : c’est le cas dans la majorité des applications liées à la voix. Dans notre cas, une telle distorsion n’était pas nécessaire et nous avons donc utilisé la distance euclidienne.
Le choix du nombre de partitions n’est pas toujours aisé. Certaines méthodes, telles que celle du coude, facilitent la tâche. Il s’agit de faire varier le nombre k de partitions initiales. Puis de représenter l’inertie (c’est-à-dire la variance intra-classe, que l’on veut la plus faible possible) en fonction de ce nombre de partitions. Lorsque l’ajout de partitions supplémentaires ne fait plus suffisamment diminuer l’inertie, on observe un « coude », qui indique le nombre optimal de partitions. Etant donné que l’initialisation des partitions est aléatoire, l’algorithme peut converger vers des solutions différentes : l’usage recommande donc de lancer plusieurs initialisations, et de retenir le cas qui minimise l’inertie. Ici, nous avons effectué 100 initialisations pour chaque k testé. Les travaux ont été réalisés sous python, avec en particulier la bibliothèque tslearn [3].
Le Graphique 3 représente l’inertie en fonction du nombre de classes. Le « coude » est assez difficile à distinguer et pourrait se situer autour de 4, 5 ou 6. Nous avons retenu k=6.
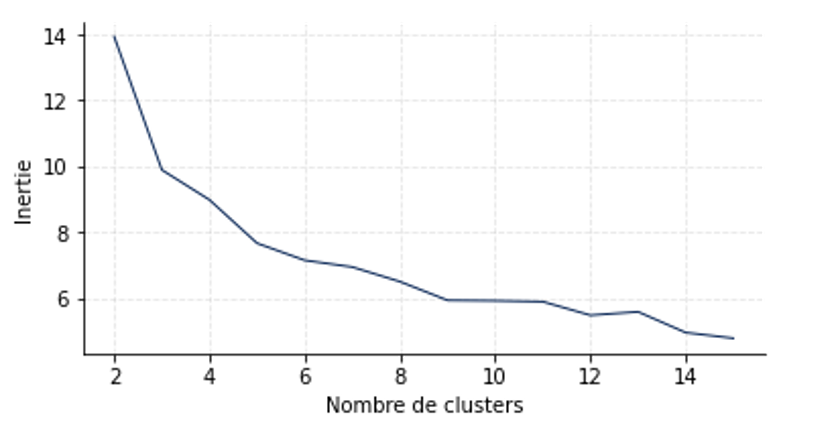
Graphique 3 : inertie en fonction du nombre de partitions.
Résultats obtenus
Le Graphique 4 présente les résultats obtenus sur nos séries temporelles. De façon générale, on observe que les partitions sont bien distinctes, et que, comme mentionné précédemment, le partitionnement s’effectue tant sur le niveau que sur la tendance (la courbe bleue est au départ très proche de la courbe rouge avant de s’en détacher sur les dernières années). Le nombre de départements rattachés à une partition varie assez fortement selon les clusters. En particulier, on note :
- le département de Paris (courbe grise) est isolé avec un nombre d’accidents pour 100 000 véhicules très élevé ;
- le département des Bouches-du-Rhône ainsi que 3 départements de la Métropole du Grand Paris (Hauts-de-Seine, Seine-Saint-Denis et Val-de-Marne) sont regroupés ensemble et sont accidentés (courbe noire) ;
- les autres partitions sont un peu plus homogènes (14 départements associés à la courbe marron, 21 associés à la courbe beige, 25 associés à la courbe rouge et 31 associés à la courbe bleue).
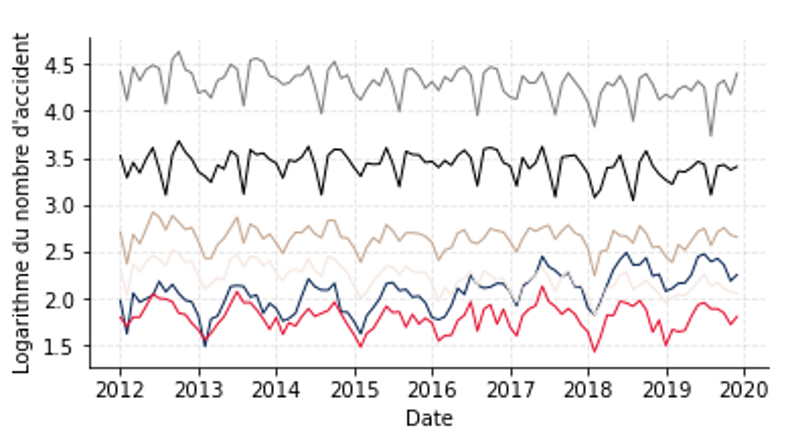
Graphique 4 : séries temporelles associées à chaque partition.
Le Graphique 5 représente le zonier final obtenu, la couleur de chaque département indiquant la partition de même couleur sur le Graphique 4.
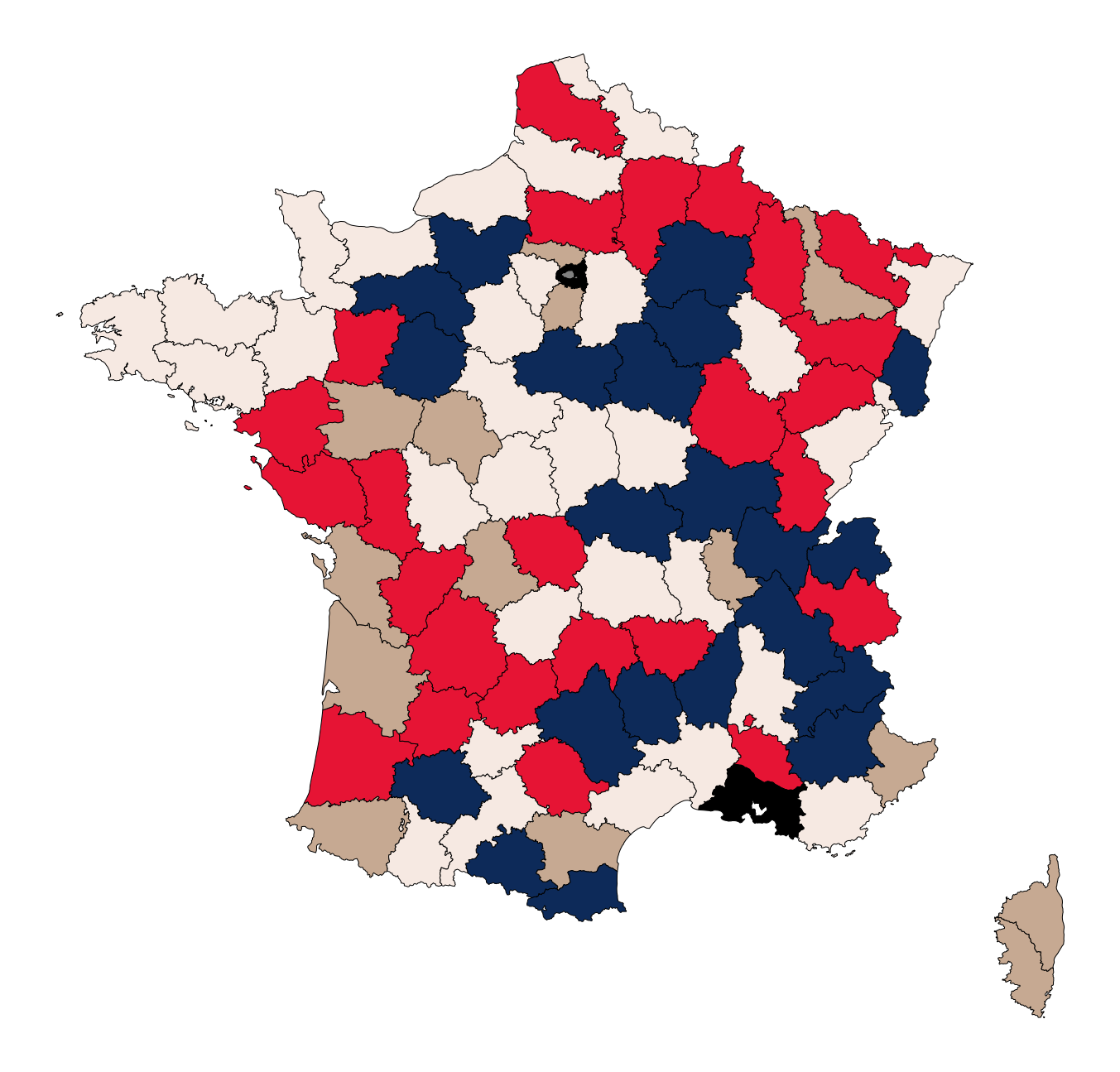
Graphique 5 : zonier final.
Notons ici que le choix effectué de raisonner en nombre d’accidents pour 100 000 véhicules reste une hypothèse déterminante. Un raisonnement en termes de nombre d’accidents (voire d’accidents mortels) pour 100 000 habitants aurait vraisemblablement donné des résultats très différents (voir les dossiers de l’ONISR par exemple).
Conclusion
Ce travail présente une méthodologie simple de partitionnement de séries temporelles sur les accidents de la route en France métropolitaine. Ce partitionnement permet de créer un zonier prenant en compte le niveau et la tendance observée sur un historique défini. Un tel travail peut être adapté à des données assurantielles et trouve une application directe en tarification automobile, via l’ajout d’une variable segmentante par exemple. Plus globalement, cette méthodologie trouve de nombreuses applications sur d’autres risques (la mortalité par exemple). De façon générale, l’exploitation de nouvelles sources de données et la sophistication des modèles doivent permettre « d’augmenter la finesse et le champ d’appréciation des risques et d’en améliorer la modélisation et la maîtrise » comme indiqué dans le dossier de l’ACPR sur la transformation numérique dans le secteur français de l’Assurance [4].
***
Références
[1] Fédération Française de l’Assurance (FFA), « L’assurance française : données clés, » 2020.
[2] Dynamic Time Warping, pp. 69-84, Springer Berlin Heidelberg, Berlin, Heidelberg, 2007.
[3] Romain Tavenard, Johann Faouzi, Gilles Vandewiele, Felix Divo, Guillaume Androz, Chester Holtz, Marie Payne, Roman Yurchak, Marc Rubwurm, Krushal Kolar, and Eli Woords. « Tslearn, a machine learning toolkit for , pp. time series data« , Journal of Machine Learning Research, vol. 21, no. 118, pp. 1-6, 2020.
[4] ACPR, « Analyses et synthèses – la transformation numérique dans le secteur français de l’assurance, » 2022.