Modélisation cyber : évaluer la fréquence des incidents
Plusieurs modèles permettent de décrire la fréquence des incidents cyber. L’European Actuarial Journal (EAJ) en décrit certains.
Modèles standards
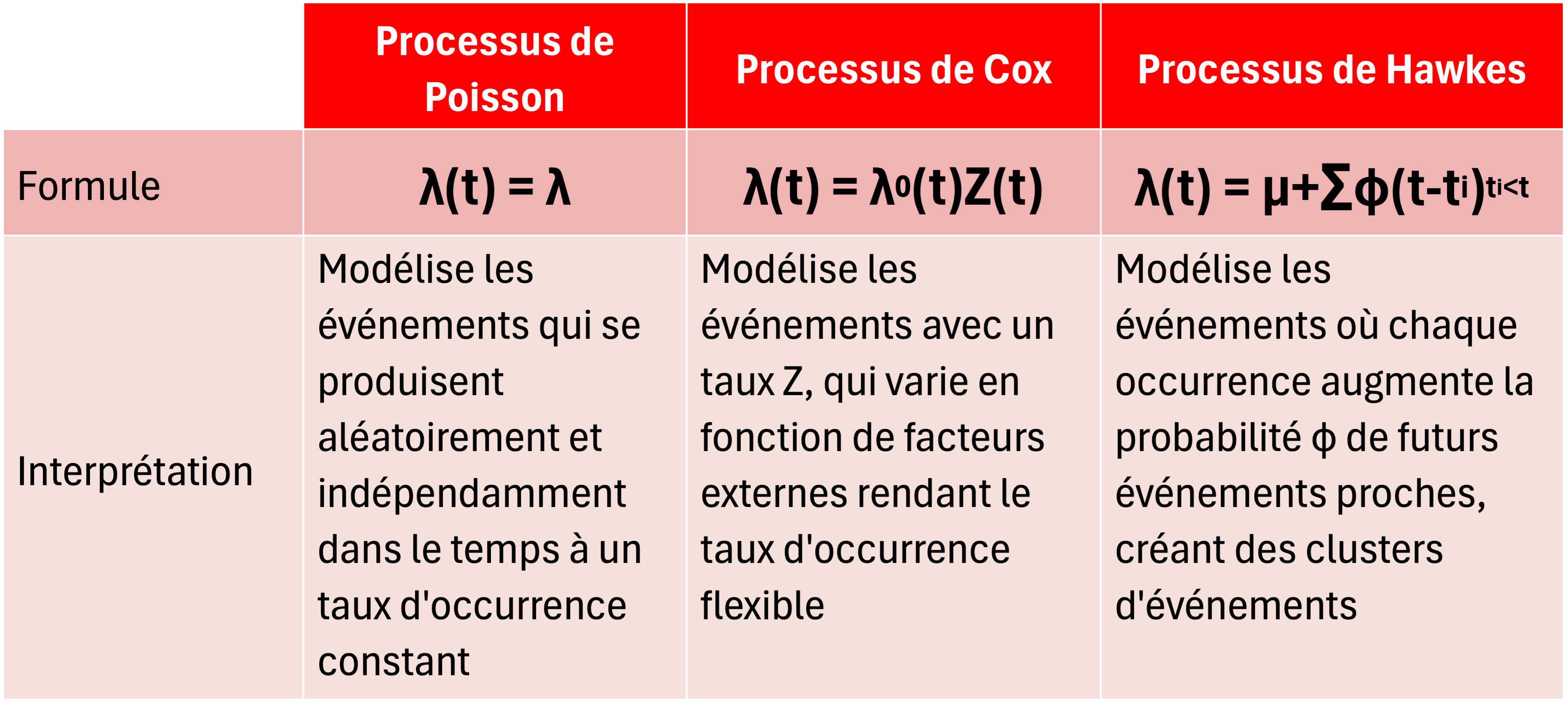
Les modèles standards, comme le Processus de Poisson et le Processus de Cox, sont fréquemment utilisés pour quantifier la fréquence des incidents cyber. Le Processus de Poisson est idéal pour les événements indépendants et aléatoires. Quant à lui, le Processus de Cox permet d’intégrer des variations du taux d’occurrence dues à des facteurs externes. Enfin, le Processus de Hawkes prend en compte les effets des incidents antérieurs sur la probabilité de futurs incidents. Une caractéristique cruciale pour comprendre les dynamiques d’attaques en cascade.
Une variante du modèle proie-prédateur
Un autre modèle permet de décrire une fréquence d’incidents. Il s’agit d’un modèle épidémiologique développé par SeaBird afin de construire un indice de risque (taux de destruction) propre à chaque entreprise du portefeuille en utilisant exclusivement le nombre de sinistres. Le modèle utilisé est une variante du modèle proie-prédateur via l’ajout d’un paramètre reflétant une tendance générale sur l’ensemble de la fenêtre d’observation. Par exemple, considérons une entreprise qui connaît son niveau de menace face au risque cyber. Elle prendra sûrement plusieurs mesures de sécurité de court terme, faisant ainsi baisser à un instant donné les attaques. Mais elle pourra également mettre en place des actions de fond efficaces sur le long terme, ce qui diminuera durablement la sinistralité cyber.
Malgré leur utilité, l’efficacité de ces modèles peut être limitée par la disponibilité et la fiabilité des données historiques, un défi majeur dans le domaine cyber où les menaces évoluent rapidement.
Modéliser la sévérité du risque cyber
Tout comme la modélisation de la fréquence, la modélisation de la sévérité du risque cyber repose fortement sur les données collectées. Le risque cyber se caractérise par une grande volatilité et les sinistres peuvent générer des coûts élevés. Il est donc essentiel de distinguer les sinistres cybers mineurs de ceux plus graves mais moins fréquents.
Cette distinction dépend alors largement du crédit que l’on donne à nos jeux de données : s’ils sont robustes, il faudra viser une approche technique. Sinon il conviendra d’opter pour une approche plus empirique.
L’approche technique et l’arbre de décision CART
Une approche technique consisterait à séparer les sinistres selon un arbre de décision CART comme dans le mémoire d’Anaïs Martinez. Les variables catégorielles décrivant le sinistre cyber (comme le type d’organisation attaquée, le type d’attaque…) sont alors regroupées dans un arbre CART. Cette méthode de segmentation permet ensuite de déterminer un coût moyen pour chaque catégorie de sinistre définie par les variables présentes dans l’arbre. Cette segmentation est intéressante car elle présente les données de façon claire et constitue une approche pertinente pour couvrir la sévérité du risque cyber. Cependant, le manque de précisions dans la base de données peut largement influencer les résultats d’un arbre CART. Il est donc nécessaire de prendre du recul sur les résultats obtenus et de les comparer avec d’autre méthodes.
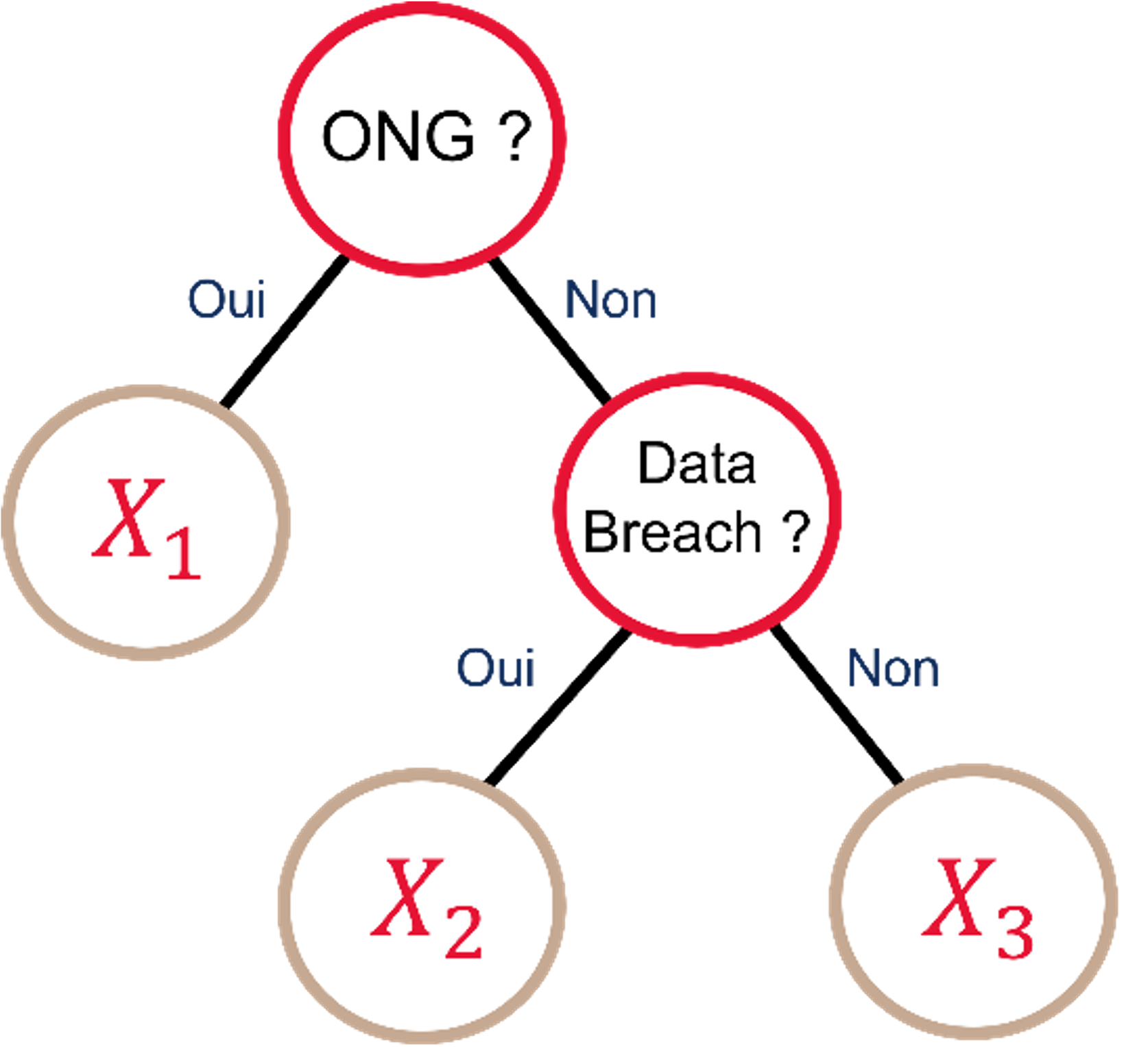
Exemple d’arbre de décision CART simplifié pour le risque cyber
La segmentation empirique
Une seconde segmentation, plus empirique et proposée par l’EAJ, consiste à « classer » les sinistres selon des cyber risk module (modules de risques cyber) prenant en compte le type d’attaque (data breach, fraudes, interruption de business…). Puis, un seuil ![]() est choisi pour chaque
est choisi pour chaque ![]() pour diviser les sinistres de chaque module en deux catégories : small claims (sinistres attritionnels) et large claims (sinistres importants). On a ainsi :
pour diviser les sinistres de chaque module en deux catégories : small claims (sinistres attritionnels) et large claims (sinistres importants). On a ainsi :
(1) 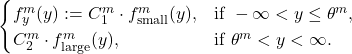
Puis on modélise séparément la sévérité des deux types de sinistres grâce aux densités ![]() et
et ![]() en utilisant des modèles classiques. L’intérêt de cette méthode porte sur le choix du seuil
en utilisant des modèles classiques. L’intérêt de cette méthode porte sur le choix du seuil ![]() , qui peut reposer sur des fondements techniques selon le module 𝑚 (si les données sont solides) ou empiriques en cas de données peu pertinentes. Cependant, cette méthode implique d’avoir un recul suffisant sur la qualité des données.
, qui peut reposer sur des fondements techniques selon le module 𝑚 (si les données sont solides) ou empiriques en cas de données peu pertinentes. Cependant, cette méthode implique d’avoir un recul suffisant sur la qualité des données.
Dynamique de propagation des incidents cyber
Le risque cyber présente un caractère systémique : le nombre d’attaques varie en fonction du système concerné. Ainsi, pour modéliser l’évolution des attaques du système, on peut faire le parallèle avec un risque de pandémie : les individus sont connectés entre eux par des flux financiers et des systèmes informatiques. Leur propre vulnérabilité au risque dépend alors de la vulnérabilité de leur voisin. Plusieurs systèmes de connexions entre individus et entreprises existent :
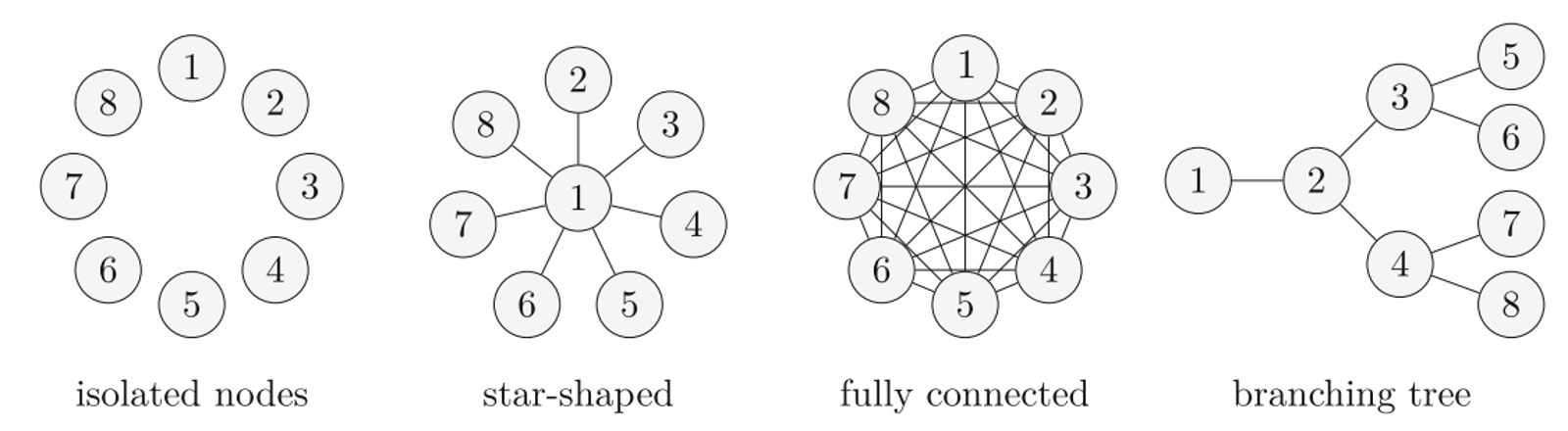
Ces systèmes de connexion font ainsi varier la façon dont les individus propagent la pandémie cyber. Par exemple, dans la structure de réseaux isolated nodes (nœuds isolés), aucun individu n’est connecté avec les autres, une attaque cyber ne se propage pas entre les individus. A l’inverse, dans une structure de type fully connected (complètement connecté), chaque attaque cyber ciblant un individu a des chances de se propager à un autre individu.
Modèles SIS et SIR
Comprendre la structure des réseaux permet par la suite de modéliser la propagation d’une attaque. Pour ce faire, plusieurs modèles sont à notre disposition. Les modèles épidémiologiques principaux pour modéliser le caractère systémique du risque cyber sont le modèle SIS (Susceptible-Infected-Susceptible) et le modèle SIR (Susceptible-Infected-Recovered).
Dans le modèle SIS, un individu de la classe Susceptible (i.e. susceptible d’être infecté) a des chances de subir une attaque cyber. Si c’est le cas, il devient alors Infected (infecté) et donc propagateur de la maladie. Ensuite un individu infecté a des chances de « guérir ». Dans le modèle SIS, celui-ci redevient alors susceptible d’être infecté (Susceptible). A l’inverse, dans un modèle SIR, l’individu infecté guérit et devient alors immunisé contre la maladie, cela représente ici la même attaque cyber.
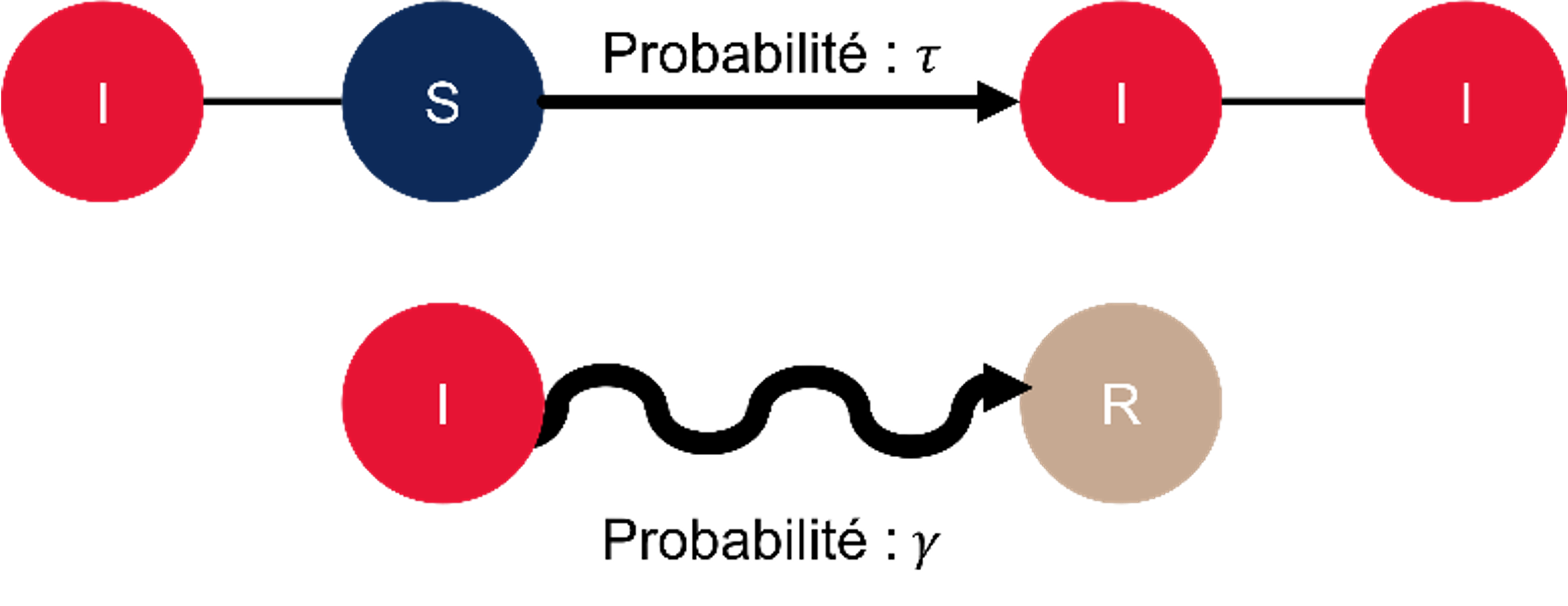
Dans le schéma ci-dessous, l’individu infecté I est connecté à un individu susceptible d’être infecté S. Il existe ainsi une ![]() que l’individu susceptible devienne infecté. En parallèle, l’individu infecté a une probabilité ϒ de redevenir susceptible d’être infecté si on se place dans un modèle SIS, ou de devenir immunisé contre la maladie dans un modèle SIR.
que l’individu susceptible devienne infecté. En parallèle, l’individu infecté a une probabilité ϒ de redevenir susceptible d’être infecté si on se place dans un modèle SIS, ou de devenir immunisé contre la maladie dans un modèle SIR.
Modèle SIS

Modèle SIR
Conclusion
Le risque cyber fait partie des risques émergents de l’assurance. Il reste mal couvert en raison de la sous-estimation du risque par encore trop d’entreprises. Et de l’insuffisance de la qualité des offres assurantielles.
La théorie nécessaire pour mieux appréhender ce type de risques existe. Mais les données disponibles sont peu nombreuses, insuffisamment détaillées et peu robustes. La volatilité des risques cyber interdit de plus de s’appuyer sur une réelle profondeur d’historique. Dans ce contexte, il est hasardeux de calibrer des modèles avec trop de paramètres. Ce serait pourtant nécessaire pour des risques aussi complexes.
Une approche plus pragmatique est donc à privilégier, soit par des scénarios soit par des calibrages à dire d’expert, sur des modèles épidémiologiques par exemple. L’appel à des experts de la cybersécurité pourrait alors renforcer significativement la compréhension des risques couverts.
Mais quelle que soit l’approche, une veille permanente reste nécessaire. Une évolution du tarif et des garanties peut être nécessaire pour suivre celle des risques cyber.
Tous les articles de notre dossier
- Assurance cyber, un marché encore embryonnaire
- Risque Cyber – de quoi parle-t-on ? Lexique
- Assurance cyber, un cadre législatif encore incomplet
- Les données disponibles, défi majeur dans la gestion des risques cyber
- Assurance cyber, une modélisation actuarielle en plein essor